Portfolio management maturity models can be a great enabler in making process improvements. Higher maturity often translates into a greater realization of the benefits of PPM. PPM maturity models are very useful for assessing the current state of the portfolio processes and how to arrive at a higher level of maturity.
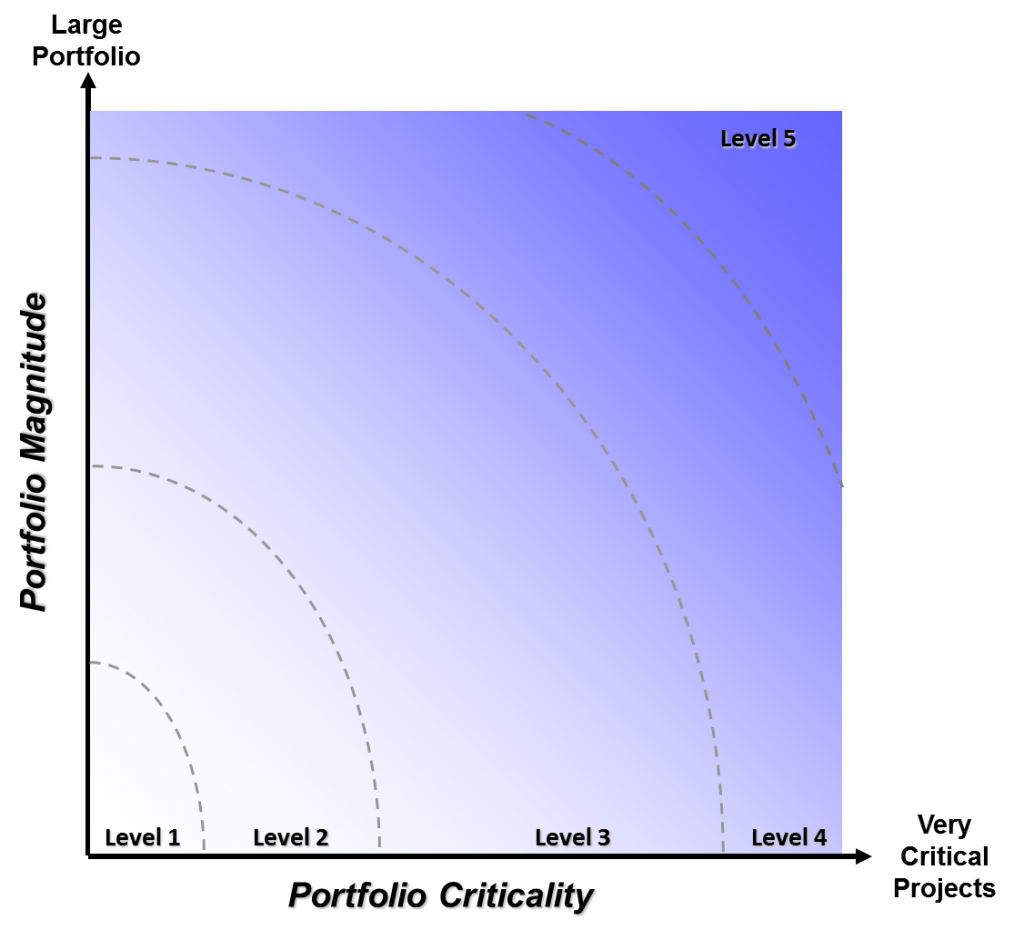
However, identifying the end state (also known as ‘future state’) portfolio processes has rarely been discussed in portfolio management literature. The common thought has been to endeavor to reach the highest level of maturity possible. Until now, there has been little acknowledgement that some organizations may not need to strive for level 5 (“optimized”) maturity (an elusive state of maturity to say the least). However, organizations can make a general determination of where their portfolio processes need to be in order to have a legitimate competitive advantage. Having this understanding gives the organization a realistic target for improvement. Such a determination can be made based on two important factors: project criticality (the importance of projects to the organization) and portfolio size (probably in dollars, but for the time being will not be quantified). In order to make a realistic assessment of future state portfolio processes, the portfolio management team first needs to make an honest assessment of project criticality (not an easy task).
The chart below is a conceptual chart depicting an organization’s portfolio maturity goal dependent on the portfolio’s criticality (along the x-axis) and the portfolio magnitude (along the y-axis). The target for many organizations would probably fall into the “Defined” stage (level 3). For some organizations with either short project lifecycles or low criticality, a level 2 (“Developing” stage) process may be sufficient. For the few organizations where projects may actually lead to increased revenue, a level 4 (“Proactive” stage) process may be necessary.